Unconditional Diffusion

0 符号定义

记图片为x,在扩散模型中，通过给 x0 逐步添加噪音得到一个图片序列x0,x1,x2,...,xT。 其中 x0表示输入图片，即不含噪音的初始图片，xT表示各项同性的高斯噪音。
前向加噪音过程:q(xt|xt−1) 表示 以 q 为加噪音方法,对 xt−1 加噪音获得 xt
后向去噪过程: p(xt−1|xt) 表示 用神经网络 p 表示对 xt去噪得到 xt−1

1 推导

1.1 前向过程

设β为加噪过程的超参数，用来控制加噪音量。 给定 β 的最小和最大值，通常为[0.0001,0.02]， 加噪音过程可以表示为

q(xt|xt−1)=N(xt;1−βtxt−1,βtI)=1−βtxt−1+βtϵ

在等式的右边 N 表示正态分布， xt 表示输出， 1−βtxt−1 表示均值， βtI表示方差, ϵ 从 N(0,1) 中采样。

重新整理一下参数:

αt=1−βtα―t=∏s=1tαs

那么

q(xt|xt−1)=αtxt−1+(1−αt)ϵq(xt−1|xt−2)=αt−1xt−2+(1−αt−1)ϵ

从而可以从

q(xt|xt−1)=αt(αt−1xt−2+βt−1ϵ)+βtϵαtαt−1xt−2+αtβt−1ϵ+βtϵ

最后可以得到:

q(xt|x0)=α―tx0+(1−α―t)ϵ

1.2 去噪过程

pθ(xt−1|xt)=N(xt−1;μθ(xt,t),Σθ(xt,t))

从 xt预测 xt−1图片的过程是，用神经网络 μθ 预测第t步的噪音，Σθ是不含可学参数的。

1.3 损失函数

计算Varicational Lower Bound

L=−log(pθ(x0))≤−log(pθ(x0))+DKL(q(x1:T|x0)||p(x1:T|x0))改写KL散度可得=−log(pθ(x0))+logq(x1:T|x0)pθ(x1:T|x0))代入p(x1:T|x0))=pθ(x0|x1:T)pθ(x1:T)pθ(x0)得:=−log(pθ(x0))+logq(x1:T|x0)pθ(x0)pθ(x0|x1:T)∗pθ(x1:T))消去−log(pθ(x0))=logq(x1:T|x0)pθ(x0|x1:T)pθ(x1:T))改为联合概率分布=logq(x1:T,x0)pθ(x0,x1:T)

从而我们得到

L=−log(pθ(x0))≤logq(x1:T,x0)pθ(x0,x1:T)

接下来处理等式的右边:
因为:

q(x1:T,x0)=∏t=1Tq(xt|xt−1)

得到:

logq(x1:T,x0)pθ(x0,x1:T)=log⁡∏t=1Tq(xt|xt−1)p(xT)∏t=1Tpθ(xt−1|xt)=−log⁡p(xT)+log⁡∏t=1Tq(xt|xt−1)∏t=1Tpθ(xt−1|xt)连乘对数换序=−log⁡p(xT)+∑t=1Tlog⁡q(xt|xt−1)pθ(xt−1|xt)提出第一项=−log⁡p(xT)+∑t=2Tlog⁡q(xt|xt−1)pθ(xt−1|xt)+log⁡q(x1|x0)pθ(x0|x1)贝叶斯重写=−log⁡p(xT)+∑t=2Tlog⁡q(xt−1|xt,x0)q(xt|x0)pθ(xt−1|xt)q(xt−1|x0)+log⁡q(x1|x0)pθ(x0|x1)分解中间项=−log⁡p(xT)+∑t=2Tlog⁡q(xt−1|xt,x0)pθ(xt−1|xt)+∑t=2Tlog⁡q(xt|x0)q(xt−1|x0)+log⁡q(x1|x0)pθ(x0|x1)化简第三项=−log⁡p(xT)+∑t=2Tlog⁡q(xt−1|xt,x0)pθ(xt−1|xt)+log⁡q(xT|x0)q(x1|x0)+log⁡q(x1|x0)pθ(x0|x1)化简=log⁡q(xT|x0)p(xT)+∑t=2Tlog⁡q(xt−1|xt,x0)pθ(xt−1|xt)−log⁡pθ(x0|x1)改写为KL=DKL(q(xT|x0)||p(xT))+∑t=2TDKL(q(xt−1|xt,x0)||pθ(xt−1|xt))−log⁡pθ(x0|x1)

第一个KL散度里面q不含可学习参数，可以忽略不计。
第二个KL散度地面，在“贝叶斯重写”的步骤中，加上了x_0的条件，使得KL散度里有两个xt−1|xt 存在。 然后我们要把这个KL散度规划成一个均方误差。

你们会推公式的人真的像在变魔法。

=DKL(q(xT|x0)||p(xT))+∑t=2TDKL(q(xt−1|xt,x0)||pθ(xt−1|xt))−log⁡pθ(x0|x1)

从1.2节#1.2 去噪过程可知

pθ(xt−1|xt)=N(xt−1;μθ(xt,t),Σθ(xt,t))q(xt−1|xt)=N(xt−1;μt(xt,t),βtI)

经过一些省略的操作最后将损失函数化简为

Lsimple=||ϵ−ϵθ(xt,t)||2

2 Training and Sampling

picture/Pasted image 20240404143558.png

训练时: 随机采样加噪步数1-T，前向传播得到xt,将xt,T输入到网络中得到噪音ϵ′,用MSE做损失函数。

注意网络预测到的是噪音ϵ

推断时:随机生成一个正态分布的图片，进行T步循环。 循环体内 预测出噪音后，用t步图片减去噪音，再除去方差得到t-1步图片。

3 Comments

为什么余弦的加噪音过程要比线性的加噪音过程效果更好？
我认为直观的解释有两点:

  1. 参考cosine positional encoding,余弦噪音可以让模型学习一个潜在的和t相关的噪音预测能力
  2. 余弦噪音在每一步上噪音量不同，模型需要对输入的图片的噪音量有所感知，换句话说，避免模型short cut

4 DDPM implementation

To fill the gap between formulas and codes

注意： x0是归一化后的图片,范围在[-1,1]

4.1 前向过程

前向过程最终的目标是给定按照给定策略加噪音得到第t步图片的过程。
给定第t-1步的图片，可以得到第t步的图片:

q(xt|xt−1)=N(xt;1−βtxt−1,βtI)=1−βtxt−1+βtϵ

1−βtxt−1为均值，βtI为方差。

前向过程的输入是图片x0,最大前向传播步数:N。按照上式计算xt需要进行n次迭代。 但是参考1.1的推导，可以得到将循环优化掉:

q(xt|x0)=α―tx0+(1−α―t)ϵ

因此这个函数可以定义为:

def sample_forward(x_0,t,alpha_bars):
	eps = torch.rand_like(x_0)
	x_t = torch.sqrt(alpha_bars[t]) * x_0 + \
			torch.sqrt(1-alpha_bars) * eps 
	return x_t

其中alpha_bars是由采样策略决定的数组，长度为t。

这个函数是一个torch style的伪代码，为了简洁所以没有用常见的类定义方法。

4.1.1 采样策略

采样策略即决定第t步噪音的方差和均值的超参数，不同的采样策略会影响加噪音的最大步数N。 举例两种最简单的采样策略：线性采样和余弦采样

超参数:

线性采样

betas =torch.linspace(min_beta, max_beta,\
		n_timestep, dtype=torch.float64)

余弦采样

timesteps = (torch.arange(n_timestep + 1, dtype=torch.float64) / 
			 n_timestep + cosine_s)
alphas = timesteps / (1 + cosine_s) * np.pi / 2
alphas = torch.cos(alphas).pow(2)
alphas = alphas / alphas[0]
betas = 1 - alphas[1:] / alphas[:-1]
betas = np.clip(betas, a_min=0, a_max=0.999)

采样完成betas之后，还需要预先计算alpha_bars的值备用:

αt=1−βtα―t=∏s=1tαs

实现为:

alphas = 1- betas
alpha_bars  = alphas.cumprod(dim=0)
#视情况可以给alpha_bars首位插入一个1，对齐下标用

4.2 后向过程

后向过程的目标是从噪音中进行N步去噪生成一张图片:
由加噪音过程：

xt=1−βtxt−1+βtϵ

得到去噪音过程:

xt−βtϵθ(xt−1,t)1−βt=xt−1

在实验中，简化噪音方差为1可以减少计算量和提升效果
从而得到:

def sample_backward(self,x,t)
        if t== 0:
            noise = 0
        if simple_var:
            var = self.betas[t]
        else:
            var = self.betas[t] * self.alpha_bars[t] * (1-self.alpha_bars_prev[t])/(1-self.alpha_bars[t-1])

        noise = torch.rand_like(x_t) * torch.sqrt(var)
        eps = net(x_t,t)

        mean = (x_t -(1 - self.alphas[t]) / torch.sqrt(1 - self.alpha_bars[t]) *eps) / torch.sqrt(self.alphas[t])

        x_t_prev = mean + noise
        return x_t_prev

5 DDIM implementation

DDIM是对DDPM采样进行加速的实现

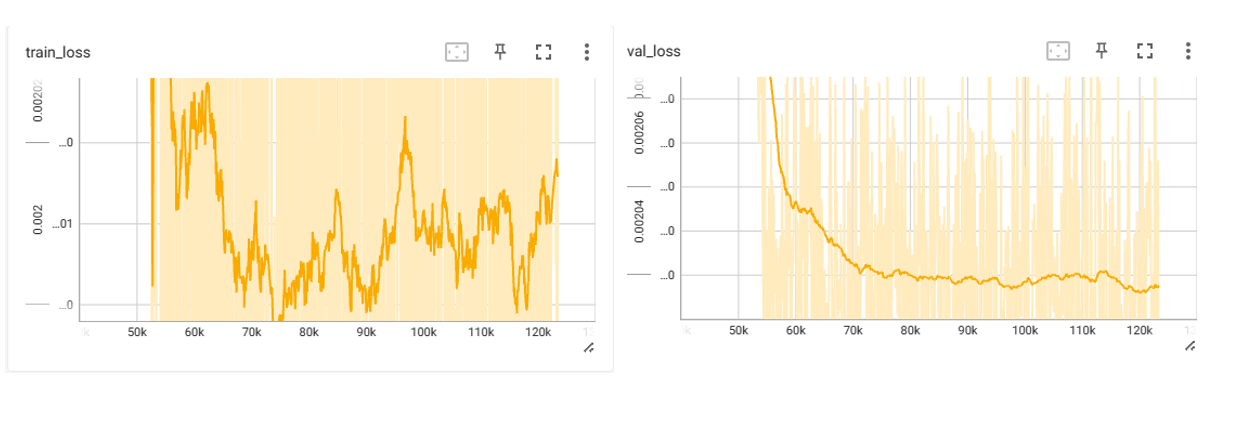
MNIST 实验结果

400个epoch batch_size=512
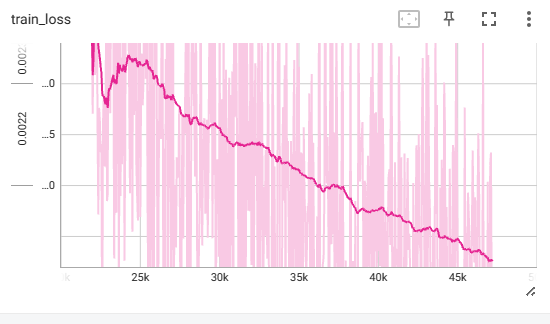
picture/Pasted image 20240502121304.png

1200个epoch batch_size=512
picture/Pasted image 20240502154537.png

参考文献

https://zhuanlan.zhihu.com/p/642006035